통계, 모델링

sYOUNG_DA 2025. 3. 4. 15:25

정규분포(Normal Distribution)는 통계학에서 가장 중요한 확률 분포 중 하나로 여러 데이터 값을 뽑았을 때 평균값(기댓값) 주변에 데이터가 가장 많이 몰리고 평균에서 멀어질수록 데이터가 점점 줄어드는 형태를 보이는 분포입니다.

즉, 정규분포는 대부분의 데이터가 평균 근처에 위치하고, 평균에서 멀어질수록 데이터 개수가 점점 줄어드는 종 모양의 대칭적인 분포 입니다.

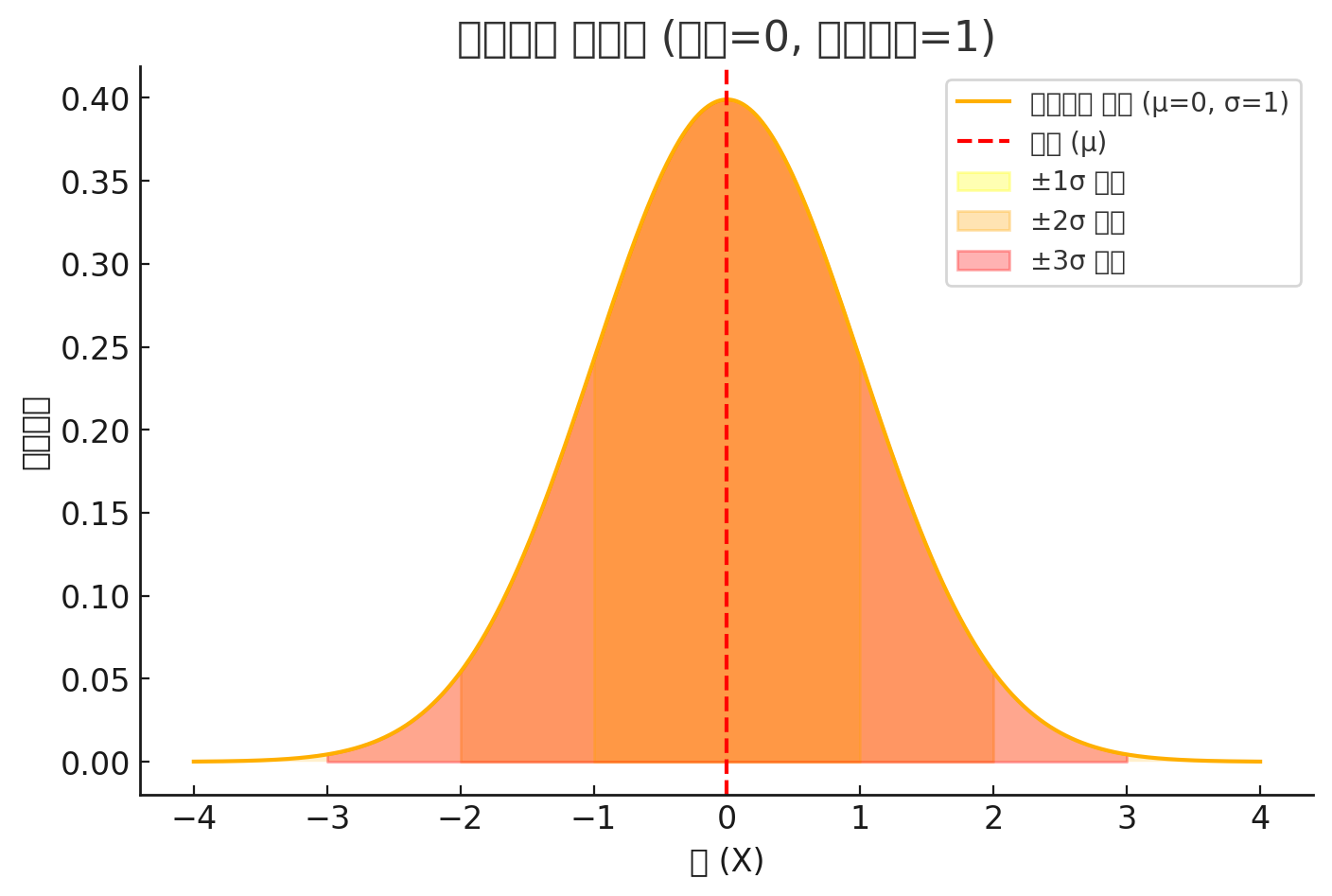
정규분포를 이해하면 통계의 개념이 이해될 것이다.

통계를 쉽게 설명하면

통계란 전체 모집단의 특성을 유추하는 학문입니다. 하지만 모집단의 모든 데이터를 수집하는 것은 현실적으로 어렵거나 비효율적이므로, 일부 데이터를 표본(Sample)으로 선정하여 분석합니다. 이를 통해 전체 모집단을 대표하는 통계를 계산할 수 있으며, 전수조사를 하지 않아도 의미 있는 결론을 도출할 수 있도록 도와주는 학문입니다.

가설검증은 어떤 생각(가설)이 맞는지 확인하는 과정

✔ 귀무가설 (H₀): 기존에 믿고 있는 것
✔ 대립가설 (H₁): 새로운 주장이 맞다고 하는 것

P-value

P-값은 우리의 실험 결과가 우연히 일어날 확률이에요.
즉, 귀무가설이 맞다고 가정했을 때, 우리가 얻은 데이터처럼 극단적인 결과가 나올 확률을 의미해요.

예시) 돼지 농장

농장주인은 돼지 10,000마리의 평균 체중이 100kg이라고 주장함.
하지만 돼지들이 너무 말라 보여서 이 말이 사실인지 의심됨.
그래서 몰래 100마리의 체중을 측정해서 확인해 보려 함.

이제, 이 데이터를 통해 귀무가설이 맞는지(P-값을 통해 검증) 해보면 맞는지 확인 가능

가설 설정

✔ 귀무가설 (H₀): 돼지들의 평균 체중은 100kg이다.
✔ 대립가설 (H₁): 돼지들의 평균 체중은 100kg이 아니다.

실험 및 P-값의 의미

만약 100마리의 평균 체중이 100kg에 가까우면, 농장주인의 말이 맞을 가능성이 큼 (귀무가설 유지).
하지만 100마리의 평균 체중이 70kg처럼 낮다면? 🤔
- 이 결과가 "우연"인지 아닌지 확인해야 함.
- 여기서 등장하는 게 바로 P-값!

P-값의 의미
P-값은 귀무가설이 참일 때, 우리가 얻은 실험 결과처럼 극단적인 값이 나올 확률!

P-값 계산 및 해석

P-값이 5% 이상 (P > 0.05)
→ 이런 결과(평균 70kg)가 나올 확률이 높음 → 돼지 평균 체중이 100kg일 가능성이 큼 (귀무가설 유지)

P-값이 5% 미만 (P < 0.05)
→ 이런 결과가 우연히 나올 확률이 5%도 안 됨 → 돼지 평균 체중이 100kg이 아닐 가능성이 큼 (귀무가설 기각)

결론:
만약 우리가 측정한 100마리의 평균 체중이 70kg이고, P-값이 0.01(1%)라고 하면?
"이런 결과가 우연히 나올 확률이 1%밖에 안 되네! → 농장주인이 거짓말할 가능성이 큼
귀무가설을 기각하고, 돼지들의 평균 체중이 100kg이 아닐 가능성이 크다고 결론 내릴 수 있음

한 문장으로 정리!

P-값이 작을수록(5% 미만일 때), 귀무가설을 기각하고 새로운 주장을 받아들일 가능성이 커짐

돼지들이 말라 보이면 실제 평균 체중이 낮을 가능성이 크고, P-값이 작으면 농장주인의 말이 틀렸다고 판단할 수 있음

t-test

t-검정(t-test)은 두 개의 그룹 평균을 비교해서 차이가 있는지 확인하는 통계적 방법이다.
즉, A그룹과 B그룹의 평균 차이가 정말 유의미한지 알아보는 데 사용돼요!

예시) 약 테스트

새로운 감기약이 효과가 있는지 확인하려면?

감기약을 먹은 사람(A그룹)과 안 먹은 사람(B그룹)의 평균 회복 기간을 비교해야 한다.
그런데 평균 차이가 발생했다고 해서 무조건 "약이 효과 있다!"라고 할 수는 없다.
우연히 차이가 생겼을 수도 있기 때문이다.

그래서 t-검정을 사용하여 이 차이가 우연인지, 진짜 효과 때문인지 판단하는 것!

가설 설정

귀무가설(H₀): 두 그룹의 평균 차이는 없다.
대립가설(H₁): 두 그룹의 평균 차이가 있다.

t-값 계산(t-test)

t-값이 크면 두 그룹 간 차이가 크다는 의미!
t-값이 작으면 두 그룹 간 차이가 거의 없다는 의미!

P-값 확인(p-vaule)

P < 0.05 → 차이가 유의미함 → 귀무가설 기각(두 그룹이 다름)
P > 0.05 → 차이가 유의미하지 않음 → 귀무가설 유지(두 그룹이 같음)

t-검정의 종류

1. 독립표본 t-검정 (Independent t-test)

서로 다른 두 그룹의 평균을 비교할 때 사용
예시: 남성과 여성의 평균 키 비교

2. 대응표본 t-검정 (Paired t-test)

같은 집단에서 전/후 변화를 비교할 때 사용
예시: 운동 전/후 체중 비교 (한 사람이 다이어트 전과 후에 체중이 어떻게 변했는지 확인)

3. 단일표본 t-검정 (One-sample t-test)

한 그룹의 평균이 특정 값과 차이가 있는지 확인할 때 사용
예시: 학교 학생들의 평균 IQ가 100과 차이가 있는지 검증

F-검정(F-test)이란

F-검정(F-test)은 두 개 이상의 그룹 간 분산(variances)을 비교하는 통계적 방법이다.
즉, 그룹 간 데이터의 변동성이 차이가 있는지 확인할 때 사용됨

t-검정과 F-검정의 차이?

t-검정 → 평균 차이를 비교하는 방법
F-검정 → 분산(데이터의 퍼짐 정도)의 차이를 비교하는 방법

F-검정이 필요한 상황

1. 두 그룹의 분산 비교 (등분산 검정, Homogeneity of Variance Test)

t-검정을 하기 전에 두 그룹의 분산이 같은지 확인해야 한다.
예시: 남성과 여성의 시험 점수 분산이 같은지 확인

2. 여러 그룹의 분산 비교 (ANOVA와 연계, Analysis of Variance)

3개 이상의 그룹 간 차이를 비교할 때 ANOVA를 사용하며, 이때 F-검정이 활용됨!
예시: 세 개의 다른 다이어트 프로그램이 체중 감량 효과에 차이가 있는지 확인

✔ 등분산(Homoscedasticity): 두 그룹(또는 여러 그룹)의 분산이 같다.
✔ 이분산(Heteroscedasticity): 두 그룹(또는 여러 그룹)의 분산이 다르다.

대립가설의 종류

✔ 대립가설에는 양측, 오른쪽 단측, 왼쪽 단측 대립가설이 있음!

✔ 양측검정(Two-tailed test) → "크거나 작거나 차이가 있는지만 확인!"
✔ 단측검정(One-tailed test) → "특정 방향(크거나 작거나 한쪽 방향만)으로 차이가 있는지 확인!"

✔ 양측검정: "두 값이 다르긴 한데, 어느 방향인지 모름!" (기준보다 클 수도, 작을 수도)
✔ 단측검정: 기준보다 더 크거나(오른쪽) 또는 더 작거나(왼쪽) 차이를 확인!

.

음......여기서 나는 양측검정과 단측검정이 이해가 되지 않는다 다시 찾아보고 이해를 해야겠다.

예시) 햄버거 가게 예시를 들어보자

한 햄버거 가게는 광고에서 우리 햄버거는 평균 200g입니다!라고 주장함
하지만 사람들이 정말 200g이 맞을까?"하고 의심하고 있다.
그래서 햄버거 몇 개를 골라 무게를 재봤어요!

------------귀무가설(H₀): 햄버거의 평균 무게는 200g이다.-------------

양측검정(Two-tailed test) 예시

햄버거가 200g보다 크거나 작을 수도 있다고 가정. 즉, 차이가 있는지만 알고 싶음
대립가설(H₁): 햄버거의 평균 무게는 200g이 아니다.

결과 예시

햄버거 평균 무게가 190g으로 나옴 → "200g과 다르다!" → 귀무가설 기각!
햄버거 평균 무게가 202g으로 나옴 → "200g과 크게 다르지 않음" → 귀무가설 유지!

언제 사용?

"차이가 있는지만 확인하고 싶을 때!"
방향(크거나 작거나)을 미리 예측하기 어려울 때!

단측검정(One-tailed test) 예시

특정 방향(크거나 또는 작거나)만 고려하는 경우!

1. 오른쪽 단측검정 (Right-tailed test) 예시

햄버거 무게가 200g보다 더 클 것이라고 주장하는 경우. 대립가설(H₁): 햄버거의 평균 무게가 200g보다 크다.

결과 예시

햄버거 평균 무게가 210g → "진짜 크네!" → 귀무가설 기각!
햄버거 평균 무게가 195g → "기대보다 작음" → 귀무가설 유지!

언제 사용?

"이게 더 클까?"를 확인할 때
예: "새로운 운동법이 기존보다 효과가 더 클까?"

2. 왼쪽 단측검정 (Left-tailed test) 예시

햄버거 무게가 200g보다 작을 것이라고 주장하는 경우
대립가설(H₁): 햄버거의 평균 무게가 200g보다 작다.

결과 예시

햄버거 평균 무게가 190g → "진짜 작네!" → 귀무가설 기각!
햄버거 평균 무게가 205g → "기대한 것보다 큼" → 귀무가설 유지!

언제 사용?

"이게 더 작을까?"를 확인할 때
예: "새로운 다이어트 약이 체중을 더 줄여줄까?"

회귀분석이란 (Regression Analysis)

회귀분석(Regression Analysis)은 어떤 변수(원인)가 다른 변수(결과)에 영향을 주는지 분석하는 방법!
쉽게 말해 X가 변하면 Y도 변하는가?를 알아보는 것이다. 데이터 속 패턴을 찾아서 미래를 예측할 때 사용한다.

X가 커지면 y는 얼마나 달라져를 궁금한 것(=기울기)

회기분석을 하면 상관계수도 알 수 있다.

매출액이 얼마나 나오는지를 확실하게 알 수 있는 부분이다.

*상관분석이란 Correlation Analysis

상관분석(Correlation Analysis)은 두 변수(X, Y) 사이의 관계가 얼마나 강한지 측정하는 분석 방법이다.
즉, "X가 변하면 Y도 같이 변하는가?"를 알아보는 것. 단, 원인과 결과(인과관계)를 알 수 있는 것은 아니다.
두 변수 사이의 관계 강도를 숫자로 표현하는 방법

상관분석은 표의 방향을 알아내는 것이다.

올라가는지 내려가는지 차이만 안다고 한다면. 회귀분석은 알고 싶은 값을 알 수 있다는 점이다.

-1부터 1까지의 값

선형회귀의 종류

단순선형회귀(Simple Linear Regression)

X 변수가 1개일 때 사용
예시: 햄버거 가격(X) → 판매량(Y)

방정식: Y=a+bXY = a + bX

다중선형회귀(Multiple Linear Regression)

X 변수가 여러 개일 때 사용
예시: 햄버거 가격(X₁), 광고비(X₂), 날씨(X₃) → 판매량(Y)

방정식:

Y=a+b1X1+b2X2+b3X3Y = a + b_1X_1 + b_2X_2 + b_3X_3

결정계수(R²)란

결정계수(R², R-Squared)는 회귀분석에서 모델이 데이터를 얼마나 잘 설명하는지 나타내는 지표
회귀선이 실제 데이터를 얼마나 잘 맞추는지 측정하는 값
0부터 1 사이의 값을 가짐 (0 ≤ R² ≤ 1)
R² 값이 클수록 예측 모델이 데이터를 더 잘 설명한다는 의미

높으면 높을수록 좋다!

(R은 상관계수)

상관계수와 결정계수의 차이

상관계수(r): 두 변수 간의 관계(관련성)를 측정하는 지표
결정계수(R²): 회귀 모델이 데이터를 얼마나 잘 설명하는지 측정하는 지표
R² = r² 관계로 연결됨!
상관계수가 높다고 해서 무조건 좋은 회귀 모델이 되는 것은 아님! (인과관계 아님!)

단순 선형 회귀는 하나의 변수로만 설명하기 때문에 한계가 있다.

따라서, 다중 선형 회귀 분석을 통해 단순 선형 회귀의 문제점을 보완할 수 있다.

조정된 결정계수를 활용하여 다중 선형 회귀 분석의 설명력을 평가할 수 있다. 또한, 회귀 모형의 유의성을 판단하기 위해 F-검정의 p-value를 확인하며, p-value가 0.05 미만이면 회귀 모형이 통계적으로 유의미하다고 볼 수 있다

값을 하나로 정하면 단순 선형회기,

매출

광고비

교육비

판매수량

고객

제품수

직원수

이런걸 다 잡으면 다중 선형 회기 분석이다.

조정된 결정계수?

계수, 변수, 상수

표준오차와 표준편차란 ?

표준 편차 → 데이터가 퍼진 정도!
표준 오차 → 평균이 얼마나 정확한지!

시계열

시간의 흐름에 따라 발생된 데이터를 분석하는 기법

주가, 매출액 등등임

지수 평활법

시간에 따라 변하는 데이터를 예측하는 방법 중 하나임 특히, 최근 데이터에 더 큰 가중치를 주고 과거 데이터를 점점 덜 반영하는 방식이다.

쉽게 말하면, "과거 데이터도 중요하지만, 최근 데이터가 더 중요하다!"

시계열 데이터를 부드럽게 만들어서 추세를 보기 쉽게 하기 위해

단순 지수 평활법 (Simple Exponential Smoothing, SES)

추세(Trend)나 계절성(Seasonality)이 없는 데이터에 사용!

예) 매일 판매되는 우유 개수 예측 (큰 변화 없음)

2. 이중 지수 평활법 (Holt’s Exponential Smoothing)

추세(Trend)를 고려하는 방법

예) 시간이 지날수록 매출이 증가하는 경우

3. 삼중 지수 평활법 (Holt-Winters Exponential Smoothing)

계급 : 변량을 일정한 간격으로 나눈 구간

계급을 정할 때에는 변량의 최소, 최대를 고려한다

도수 Frequency

각 계급에 속하는 자료의 수

측정하다-> 도, 숫자-> 수 =횟수를 잰다는뜻

도수분포표 Frequency Distribution Table

어떤 값이 몇 번 나왔는지 정리한 표를 도수분포표

상대도수 Relative Frequency

전체에서 특정 값이 차지하는 비율을 나타내는 거야.예를 들어 위의 표에서 전체 10명 중에서 사과를 좋아하는 사람은 4명이야.그러면 상대도수 = 4 ÷ 10 = 0.4 (40%)즉, 상대도수는 전체 중에서 차지하는 비율을 뜻해---전체에서 특정 값이 차지하는 비율

히스토그램Histogram

막대그래프 Bar Graph

히스토그램 숫자 범위(구간), 연속적인 데이터, 막대 붙어 있음

막대그래프 → 카테고리(종류), 이산적인 데이터, 막대 떨어져 있음

도수분포표를 시각적으로 나타낸것( 막대그래프로 표현함), 차이점은 도수(계급을 나눈수)가 있다는게 차이다.

평균(mean)

평균(mean) -4가지 종류

1. 산술평균 (Arithmetic Mean)

가장 흔한 **"평균"**임

계산법: (모든 값의 합) ÷ (값의 개수)
예: 10, 20, 30의 산술평균 (10+20+30)÷3=20
특징: 단순한 값의 합을 나누는 방식

2. 가중평균 (Weighted Mean)

값마다 **중요도(가중치)**가 다를 때 사용함

예: 시험에서 중간고사(40%), 기말고사(60%)를 반영할 때

중간: 80점, 기말: 90점

중요한 값이 더 크게 반영될 때 사용!

3. 기하평균 (Geometric Mean)

비율이나 성장률을 다룰 때 사용해!

계산법: 값들을 곱한 후, 루트를 씌움

예: 연도별 성장률 1.2배, 1.5배, 1.3배라면?
- 즉, 연평균 1.32배 성장한 것과 같음! 비율이 포함된 데이터에 적합!

4. 조화평균 (Harmonic Mean)

속도나 비율을 평균 낼 때 사용

표준편차

정규분포란

표준편차란 (Standard Deviation)

옆으로 얼마나 퍼져있는지 (종모양의 그래프가 뱀인지 코끼리인지 ) 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 값임 값들이 평균 주변에 몰려 있는지, 퍼져 있는지를 확인할 수 있어.

A반50, 55, 60, 65, 7060점

B반30, 45, 60, 75, 9060점

A반은 점수가 평균(60점) 근처에 모여 있음

B반은 점수가 널리 퍼져 있음

둘 다 평균은 60점이지만, B반이 점수가 더 퍼져 있어!

이때 B반의 표준편차가 더 크다고 말해!

표준편차 구하는 법

-평균을 구함

-각 값에서 평균을 뺀 값(편차)을 구함

-편차를 제곱해서 모두 더함

개수로 나눈 후, 제곱근(√)을 씌움평균을 구함

-각 값에서 평균을 뺀 값(편차)을 구함

-편차를 제곱해서 모두 더함

개수로 나눈 후, 제곱근(√)을 씌움

평균(Mean)

데이터의 대표값

편차(Deviation)

각 값이 평균에서 얼마나 차이 나는지

분산(Variance)

편차 제곱의 평균

표준편차(Standard Deviation, σ\sigmaσ)

분산의 제곱근 즉 옆으로 얼마나 퍼져있는지 (종모양이 그래프가 )

관측된 변량의 스케일을 표준화 할 수있는 좋은 수단은 ??

표준편차를 이용해서 정규분포를 그린다

뱀모양과 종모양을 같은 선상에 두고 비교할 수 없기 때문에 표준화해서 정규화를 통해서 정규분표의 형태로 만들어 줄 수있다.

정규분포

평균을 중심으로 좌우 대칭이며 평균과 표준편차에의해 곡선 모양 결정되는 연속확률분포

옛날옛날에 이박사가 있었다

이박사는 x=5라는 걸 증명하고 싶은데 증명할 방법이 없었음

그래서 1000번의 실험을 함

할때마다 4.9/4.8/5.1/5.9-----> 이런식으로 5와 비슷한 숫자가 계속 나옴

이걸 그래프로 그려보니 종모양의 그래프가 나옴

많은 실험을 통해서 이런 종모양의 그래프를 알아냄

근데 할때마다 계속 이러한 값을 계산하는게 귀찮게됨

그래서 표준으로 바꿔서 계산할 수있는 표준 정규분포를 알아냄

여기서 표준화를 써야함

정규분포 (Normal Distribution)

데이터가 평균을 중심으로 대칭적으로 분포하는 종 모양의 그래프

표준정규분포 (Standard Normal Distribution)

평균이 0, 표준편차가 1인 특별한 정규분포

표준화 (Standardization)

데이터를 평균 0, 표준편차 1로 변환하는 과정

파란색은 평균이 0이고 표준편차가 1인 정규분포

주황색 평균이 0이고 표준편차가 2인 정규분포

초록색 평균이 2이고 표준편차가 5인 정규분포

핑크색 평균이 5이고 표준편차가 3인 정규분포

표준편차가 높으면 많이 퍼져있음(옆으로 얼마나 퍼져있는지 알려주는 지표임)

모집단 (population)

조사 대상이 되는 전체 집단

모수

모집단을 요약한 수치(대한민국 국민중 여자가 몇퍼센트인지 그런 수치임 즉 우리가 알고 싶은값)

표본

모집단을 대표하는 일부

모평균 (μ)Population Mean 뮤 (μ)

모집단의 평균

표본평균 Sample Mean (엑스바 )

모분산 Population Variance-모집단의 분산

분산 (σ2) → 편차(거리)의 제곱 평균 ...모집단 전체의 평균 편차 제곱값

모집단(전체 데이터)이 평균에서 얼마나 퍼져 있는지 알려주는 숫자

예시 농구공 던지기 게임

친구 5명이 농구공을 던졌어! 각자 넣은 개수는:(2, 4, 6, 8, 10)

평균을 구하자! (2+4+6+8+10)÷5=6 즉 평균은 6임

각 값이 평균에서 얼마나 차이나는지 보자! (편차)

2 → 2−6=−4

4 → 4−6=−2

6 → 6−6=0

8 → 8−6=2

10 → 10−6=4

편차를 제곱해서 더하자! (음수를 없애려고 제곱하는 거임!)

(−4)2 이렇게제곱을 5개의 숫자에 해주면 = 16 + 4 + 0 + 4 + 16 = 40

개수로 나눠주자! (평균 구하기)

40÷5=8

🎯 결과: 모분산 = 8

표본분산 s2

표준편차 (σ) → 데이터가 평균에서 얼마나 퍼져 있는지

엑셀에서는 분산을 구할때 아래와 같은 식을 쓴다.

var.p

var.s

stdev

(여기에서도 stdev.p와 s로 나누어짐 )

Variance of population----> var.p

-우리가 모집단의 데이터를 전부 가지고 있다

Variance of sample----> var.s

-우리가 표본집단의 데이터만 가지고 있다.

standard deviation (표준편차)

추정(++표본)

표본들의 변량을 분석함으로써 모집단이 이런 특성을 가질꺼야 유추하는 그 과정을 추정이라고함

즉 표본 추출의 목적은 모집단을 추정하기 위해서임 그래서 표본이 *****표본의 개수(데이터의 양, 변량의 개수)**가 많아질수록******커질수록 모평균에 가까워진다.

신뢰도 (+모평균)

값이 알맞는 모평균이라고 믿을 수 있는 정도

95%, 99%를 주로 사용함

표본이 커질 수록 모평균에 가까워져 정규분포 모양도 좁아진다.

즉, 표본이 커질수록 모평균의 정확한 위치를 구할 수 있다.

신뢰구간이란

모평균의 추정구간--> 신뢰도/ 표본의 수에 따라 정해짐

구간을 넓게 잡으면 모평균이 이 구간안에 있는 확률이 올라감--> 신뢰도도 올라감 (실제로 이안에 있는 확률이 높으닌깐)

그러나 구간 자체가 너무 넓으면 아무의미가 없다.

그래서 95%위험을 감수하더라도 신뢰 구간을 적당한 범주로 설정을 해서 사용하는 것이 모평균의 위치이다.

그래서 그 적정한 기줌은 95%나 99%을 자주 쓴다.

[기초 통계량]

중심 경향성 central tendency

데이터 분포에서 중심에 얼마나 몰려있느냐...중위값, 최빈값, 평균 이런것들이 있다.

퍼짐정도

자료가 얼마나 흩어져있고 얼마나 모여있는지

대표값

자료의 특성을 나타낼 수 있는 대표성을 띄는 수치

왜도 (skewness)

중심위치, 분포, 기울어진 방향과 정도 (왜도 개념)

중심위치로부터 분포가 기울어진 방향과 정도를 나타내는 척도

왜도가 <0 즉 음수일때

negative skew 라고 부르며 우편향성 가지고 있다

=0 일때는 좌우대칭이 맞다고 보고

정규분포라고 한다

-3< <3까지 좌우대칭으로 보는 수치라고 생각한다

(왜도를 나누는 기준을 절대값 3을 기준으로 한다-많이사용하는 지표이다)

왜도가 양수일때 즉 >0 좌편향을 띄며

positive skew 라고 한다.

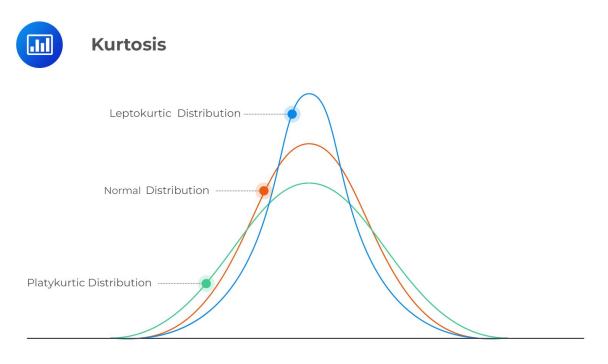
첨도 (kurtosis)

평균을 중심으로 얼마나 가까이 몰려있는지 나타내는 지표

양쪽 고리의 두터움의 정도를 나타내는 값

편차가 큰 데이터가 많을수록 커짐

이상치에 영향을 많이 받음

mode최빈값

Median중위값

mean산술평균

공분산

공분산 covariance

2개의 확률변수의 선형관계를 나타내는 값

공-> 함께

분산-> 나누다

즉 데이터가 함께 변하는 정도를 뜻하는 말

하나가 변할때 다른 하나도 같이 변하는지를 나타내는 개념임

공분산의 부호

- : 음의 상관관계----반대방향이면

0 : 상관관계 없음

+ : 양의 상관관계--같은방향이면

표본공분산

모집단 전체가 아니라 일부 데이터로 공분산을 계산할 때 사용하는 개념이다.

주의점

두 변수가 아무 관계 없는 독립 변수일 때

■ 공분산 = 0

○ 공분산 = 0

■ 두 변수가 독립은 아닐 수 있음

상관계수

두 개의 숫자 데이터가 얼마나 밀접하게 관련이 있는지를 나타내는 값이다.

즉, 하나의 값이 변할 때 다른 값도 변하는지를 측정하는거다.

상관계수의 특징

-1< <1 사이의 값의 범위이다.

1에 가까울수록 두 데이터는 강하게 움직인다.

-1에 가까울수록 두 데이터는 강하게 반대로 움직인다 (음의 상관계수)

가장 대표적인 상관계수는

피어슨의 상관계수가 있다

가장 많이 사용하는 일반적인 상관계수인데 이 값은 두 데이터가 선형적인 관계를 가지는지를 측정한다.

즉====직선관계(직선으로) 표현할 수 있는 것을 측정하는 도구임

그래서 곡선관계는 제대로 측정하지 못함.

이상치(outlier) 탐지하는 방법

1. 사분위수(IQR)을 활용한 이상치 탐지

Q1-1.5 *IQR --이 숫자들보다 크거나 작으면 이상치임

Q3 + 1.5*IQR

==조건문

=IF(OR(데이터A<이상치, 데이터B>이상치)

===이렇게 쓰면 이상치가 발견되면 1이라고 표시하고 아니면 0을 표기함

2. Z-score을 활용한 이상치 탐지

정규분포를 활용한

평균, 표준편차를 알면 정규분포를 알 수있다.

(stdev-표준편차)

정규분포를 따른다는 가정이 있어야 한다.

원래데이터를 표준화한다음 3을 기준으로 한다음 99.7%데이터를 사용하고 0.3%모든것을 이상치로 탐지하겠다라는 말임.

요금 표준화하는 방법 =데이터-평균 /표준편차(반드시 절대참조)